线性插值
线性插值方法的基本原理是根据导频位置将基系数向量分隔成各个小段,在每个小段内利用导频位置的数据通过一次函数拟合进行插值,从而得到导频位置之间的数值。插值函数如下:

线性插值方法复杂度较低,在算法性能方面的表现一般,由于其低通滤波的特性,插值得到的数值的高频成分被滤除,降低了插值得到的基系数的数值精度。然而由于操作起来比较简单,插值得到的结果也不会太差,因此也被广泛运用在实践中。


sinc函数插值
根据香农采样定理[1]我们知道,对于带限的信号,即信号的最高频率有界,当信号采样频率大于信号的最高频率的两倍时,则可以通过采样点无失真的恢复出原信号。通过采样点来恢复原信号使用的是在频域上具有理想低通特性的sinc函数。利用sinc函数对采样后的信号进行卷积,时域卷积,对应频域乘积,即是用sinc函数的经过傅里叶变换的频域形式乘以采样信号的频域表达式,由于sinc函数的傅里叶变换为窗函数,也就等效为对采样信号在频域做了一次低通滤波的操作,从而在时域上完成插值的过程。
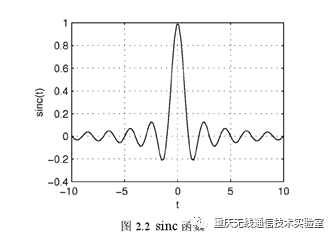

sinc函数插值的思想是通过每个导频点的值来对数据点以sinc函数的形式进行加权。由于sinc函数自身的特性,对于导频点,sinc函数的加权函数值为0;而对于数据点,则是通过各导频点的sinc函数加权值相加得到插值结果。因此最终的结果是各导频点以sinc函数进行加权不影响其他导频点的数值结果,而插值得到数据部分的基系数结果。由于sinc函数在时域上是无限的,并且其正半轴第二个零点之后的函数值都接近于0,因此通常我们忽略第二个零点之后的部分,仅截取正负半轴第二个零点之间的部分作为插值核函数,以此来降低计算的复杂度。




参考文献
[1] Hall A, Mccrorie P. Principles of Communication[M]// How to Present at Meetings, Third Edition. John Wiley & Sons, Ltd, 1995:1-7.
[2] Bharati N, Khosla A, Sood N. Image reconstruction using cubic B-Spline interpolation[C]// India Conference. IEEE, 2012:1-5.
作者简介:孙国栋,重庆大学无线通信技术实验室硕士研究生,主研方向为高速移动通信中的信道估计与插值。







