最近有个讨论:即做一元线性回归(Simple Linear Regression-SLM)时,自变量(X)和因变量(Y)是否需要符合正态分布?不符合正态分布是否可以做回归?回归模型可不可以用?
大家百度或谷歌一下,可以发现铺天盖地的结果说需要正态分布,但又语焉不详。本篇我们结合《Minitab与六西格玛管理》一书来介绍一下一元线性回归(SLM)究竟需不需要正态分布、以及前提是什么?
基本上结论是:
-
自变量(X)正态性没有任何要求;
-
因变量(Y)比较复杂,也有很多误解。有两种意见:
2.1 需要正态,但不通过检验因变量(Y)本身验证正态,而是通过残差检验来确认正态;
2.2 不需要正态,但对于给定的自变量(X),因变量(Y)的一系列观察值得分布必须正态分布。
具体而言,一元线性回归(SLM) 假定为:对自变量没有任何要求,只对因变量(Y)有以下5个假定:
-
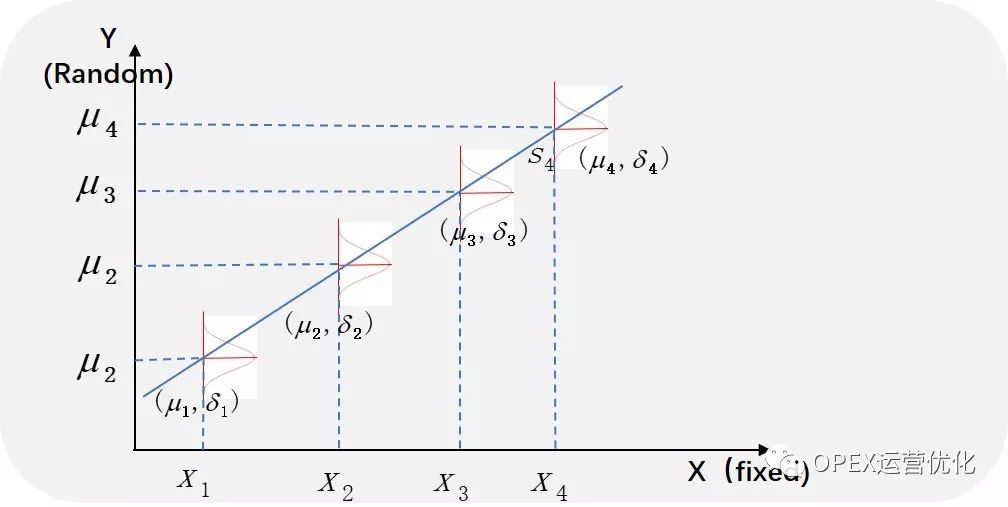
存在性(Existence):对于任何给定的X值,Y是随机变量、且其符合一定分布,并存在有限的均值和方差;
-
独立性(Independent):对因变量(Y)的要求独立性,即因变量(Y)后一次的值和前一次值没有关系;
-
线性(Linearity):自变量(X)和因变量(Y)均值是线性函数关系;

-
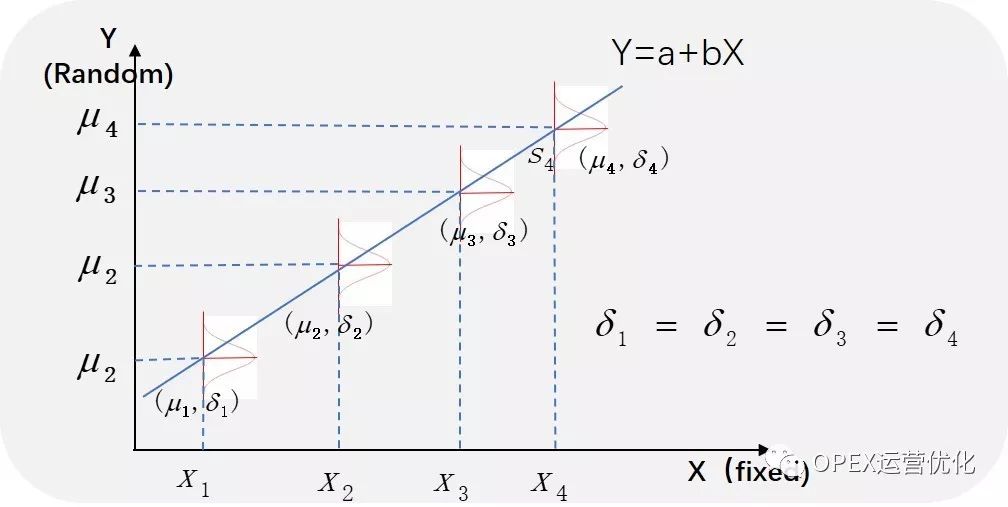
正态性(Nomality): 对于任何给定的X值,Y是随机变量,Y的观察值符合正态分布,不是说Y符合正态分布而是Y在给定X值时,Y观察到的一组数符合正态分布;如图:当X取X1时,我们观察到一组Y值,这组Y值需满足正态分布,当取X2,X3,X4时,对应的Y的三组观察值也应该符合正态分布;
-
方差齐性(Homoscedasticity):当X取任何给定值时,Y在相应X给定值处观察值的分布是方差相同的分布。如下图:当X取X1时,Y的观察到的数据组和在X2,X3,X4时观察到数据组都是正态,且等方差。
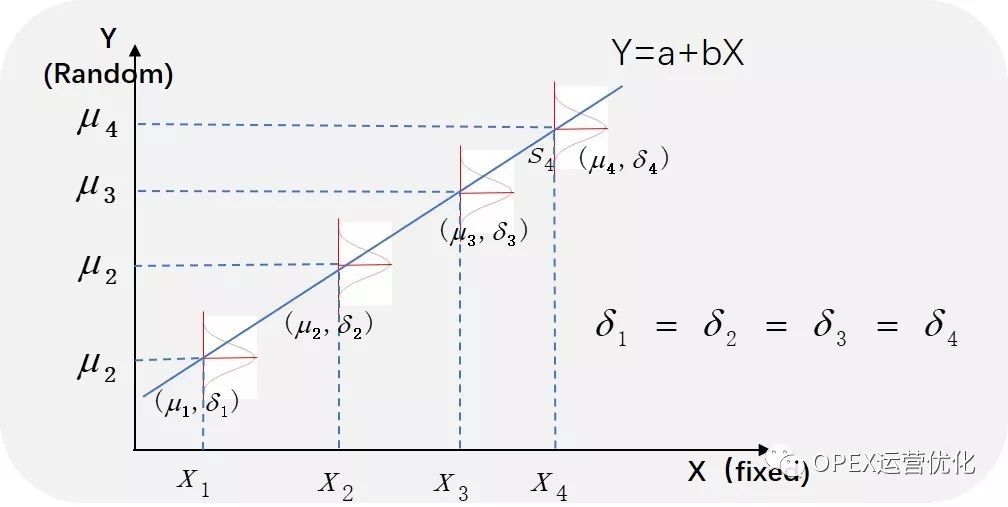
回归中是通过残差(Residual)来验证以上假设是否满足,而不是直接对因变量(Y)做正态性检验或其它验证,因为假设前提没有说因变量(Y)一定符合正态分布。
残差(Residual)定义:观察值(observed value)减去拟合值(fitted value),如下图示意:
|
自变量(X) |
观察值Y(observed value) |
拟合值(fitted value) |
残差Residual) |
|
3 |
5.5 |
5.1 |
0.4 |
|
5 |
7.5 |
7.8 |
-0.3 |
|
7 |
12.5 |
12.7 |
-0.2 |
|
12 |
24 |
24.5 |
-0.5 |
|
15 |
28.5 |
28.0 |
0.5 |
|
… |
… |
… |
… |
可以看出,如果一元线性回归模型拟合好的话,残差应该不管在X给定值在多少的情况下,残差都比较小,理想情况下:残差应该是以0为均值、一个很小数为方差的正态分布,且方差应该保持恒定。
一元线性回归(SLM)就是通过旋转找到残差方差(SSE)最小的线性模型,即最小二乘法(Least Square Method)。
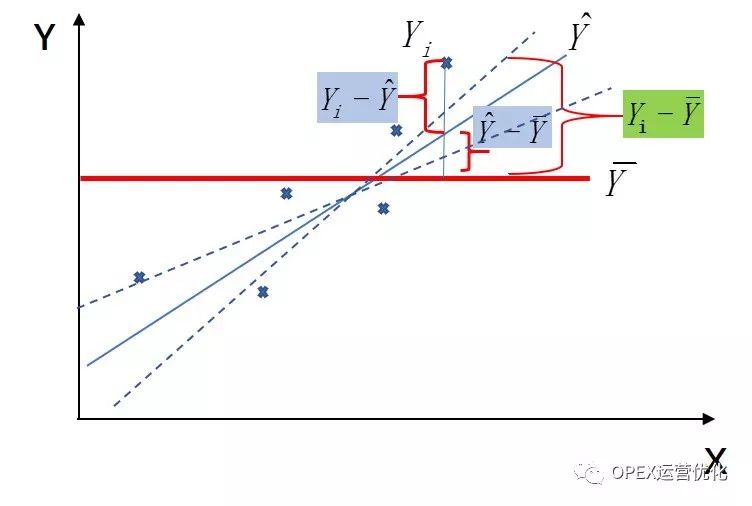
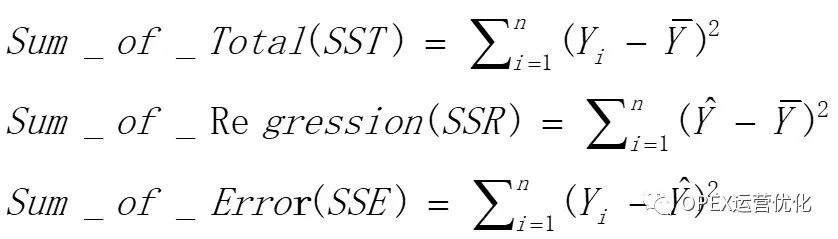
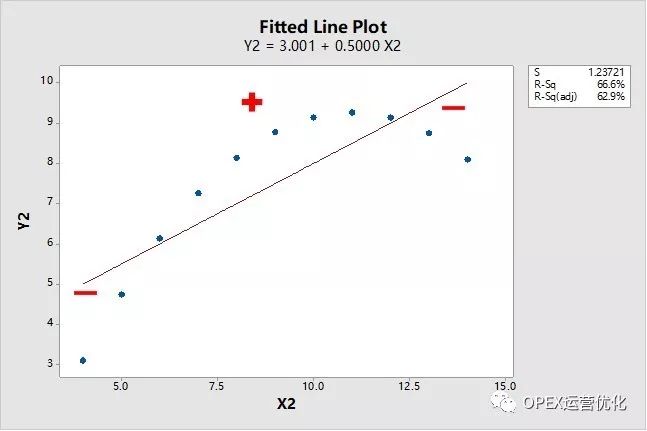
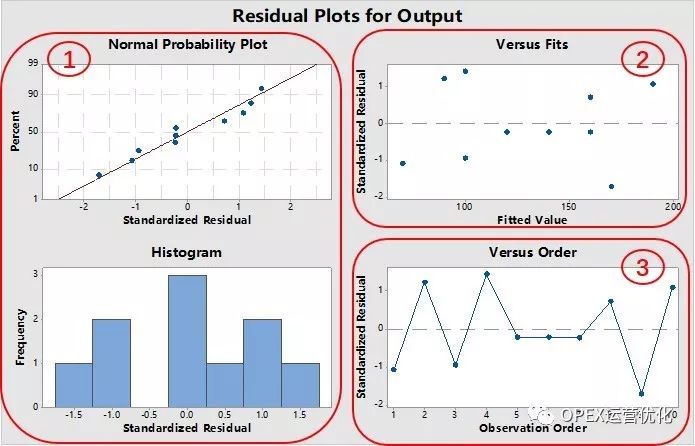
在MINITAB中作一元线性回归(SLM),具体可以通过查看残差四合一图以及残差和自变量(X)图来查看和确保Y的几个假设是否满足:
-
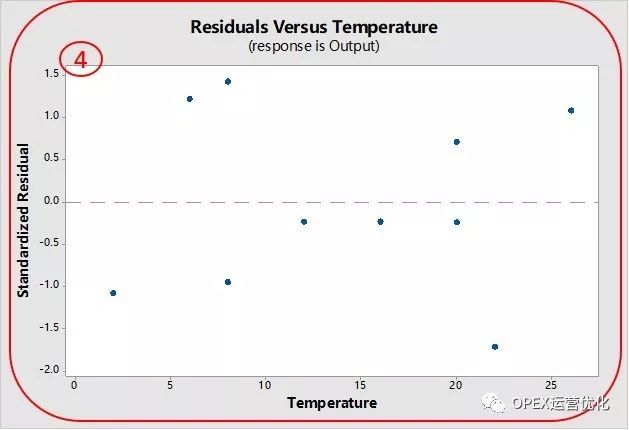
线性(Linearity):残差和Y拟合值图、残差和X的给定值图应该是不管Y拟合值多大、X的给定值多少,残差一定是以较小值为中心等方差稳定波动,没有喇叭口和弯曲。弯曲代表二元关系、非线性。(2)&(4)
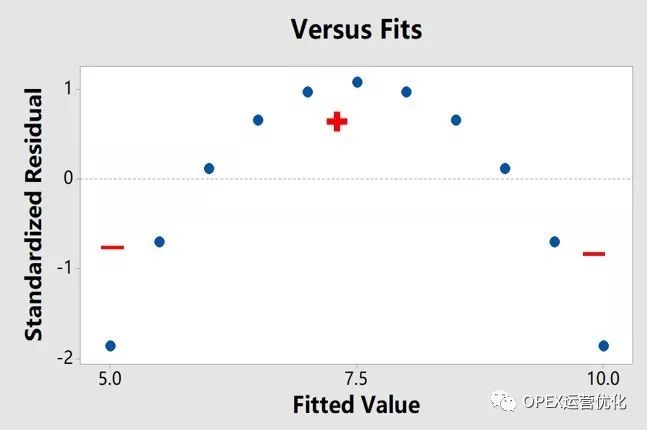
-
正态性(Normality): 残差的概率图接近直线、残差的直方图对称、钟形分布。(1)
-
方差齐性(Homoscedasticity):当X取任何给定值时,残差是一定较小值为中心等方差稳定波动,残差的时序图稳定受控。(3)
最后,一元线性回归(Simple Linear Regression-SLM)正态性的要求是指:对于给定的自变量X值,因变量Y是随机变量、Y的观察值符合正态分布,而不是因变量Y符合正态分布。







